Abstract
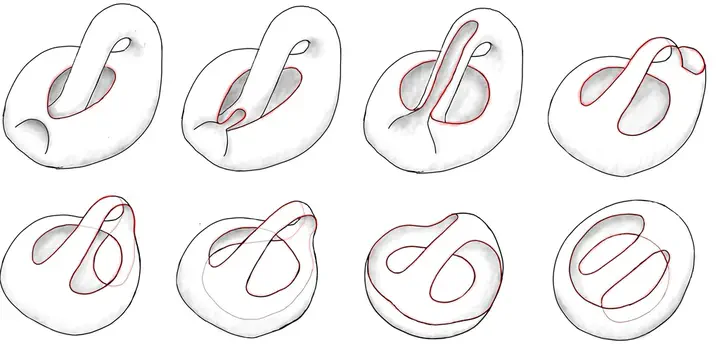
The 19th century saw the development of a new branch of mathematics, topology, which studies the properties of geometrical objects that are invariant under continuous transformations. In the subsequent decades, topology would have a great influence on the way in which artists and architects sensed and represented space. Among them, the Italian architect Vittorio Giorgini (1926 - 2010) pioneered the topology-flavoured ideas of elastic surfaces and of form as a dynamic structure. Beside his architectural works, Giorgini left a few enchanting sculptures, in which he explored the connection between shape and topology. In this paper, we first present Giorgini’s beautiful architectural designs, which were largely unrecognized in his lifetime, and they have only recently started to receive the attention they deserved. Then, we explain the topological ideas behind six of his sculptures, in a formal mathematical language. Surprisingly enough for non-mathematicians, four of his most famous sculptures - Modified Klein, Giorgini Sphere, Giorgini Torus I, and Giorgini Torus III - turn out to be topologically equivalent. This means that they can be continuously deformed into one another, even though their geometric appearances are very different from each other. We first illustrate by drawing the steps in the deformation process. Then, we provide a formal proof of the equivalence using basic notions from algebraic topology: non-orientable genus, Euler characteristic, and the classification theorem for surfaces. Giorgini designed his three-dimensional figures in-between the late 1960’s and the first half of the 2000’s. The figures only existed as bi-dimensional drawings for many years. Then, Giorgini asked David Dainelli and Alessandro Marzetti to carve alabaster sculptures from his drawings, in their artistic workshop in Volterra (Pisa, Italy), under his direct supervision. Giorgini’s sculptures represent non-orientable surfaces. Intuitively, non-orientable surfaces are one-sided: one could paint in colour the whole surface without crossing its boundary and without detaching the brush. That would not be possible for orientable surfaces such as the familiar cylinder and sphere, which are two-sided. The first sculpture we present is Modified Klein, a Klein bottle with a disk removed. The Klein bottle is a well-known and fascinating example of a non-orientable surface, which not only is one-sided, but also closed (it has no boundaries) while it does not enclose an interior. As it often happens with physical reproductions of the Klein bottle, Giorgini cut a disk around the surface self-intersection. The other three sculptures named Giorgini Sphere, Giorgini Torus I, and Giorgini Torus III are constructed through variations on the same procedure: start from a sphere (a torus), cut away portions of the surface to make a cylinder, then connect the top and bottom boundaries of the cylinder with a strip without twisting, to get a non-orientable surface. What would sound surprising to a non-topologist is that, beside being neither spheres nor toruses, the three sculptures are topologically equivalent to Modified Klein. All four sculptures are non-orientable surfaces with one boundary, and after some calculations one can verify they all have non-orientable genus equal to 2: being the non-orientable genus a topological invariant, the four sculptures share the same topological type. In our paper, for illustration purposes, we draw eight steps in the deformation process which takes Modified Klein to Giorgini Torus I. Finally, we report on the topological type of two other sculptures: Giorgini Torus II, a non-orientable surface with three boundaries which has the topology of a Moebius strip minus two disks, and Giorgini Torus IV, a non-orientable surface with two boundaries which has the topology of a sphere with five holes, three of which are capped by Moebius strips. Bridges 2020 presentation (.pptx) Deforming Modified Kein into Giorgini Torus I (.mp4)
Vittorio Giorgini: Architetture d’Alabastro, by Duccio Benvenuti