Relight:
A Compact Representation
of Relightable Images
for the Web
Federico Ponchio, Massimiliano Corsini, Roberto Scopigno
Relightable Images
Camel
Reflectance
Transformation
Imaging
- Fixed view point
- Arbitrary lighting
- In practice directional light
Reflectance Transformation Imaging (RTI)
[R, G, B] = f(x, y, θ, φ)

Sampling the function
Light dome

Manual light positioning

A stack of images
~50-100 images ~500MB!

All the pixels for one light

All the lights for one pixel

(a column in the stack)
Challenges
- Interpolation/Fitting
- Compact representation
- Efficient rendering
Sampled function*


*Actually one function per channel RGB
Continuous function*


*Which interpolation/approximation?
Polynomial fitting

Polynomial Texture Map (2001)
(PTM)
R(l) = r0 + r1lx + r2ly +
r3lx2 + r4ly2 +
r5lxly
G(l) = g0 + g1lx + g2ly +
g3lx2 + g4ly2 +
g5lxly
B(l) = b0 + b1lx + b2ly +
b3lx2 + b4ly2 +
b5lxly
Requires 18 coefficients
LPTM
Y(l) = y0 + y1lx + y2ly +
y3lx2 + y4ly2 +
y5lxly
R(l) = r0Y(l)
G(l) = g0Y(l)
B(l) = b0Y(l)
Requires 9 coefficients
It's a weighted sum of a basis

Spherical Harmonics
vs.
HemiSpherical Harmonics (HSH)
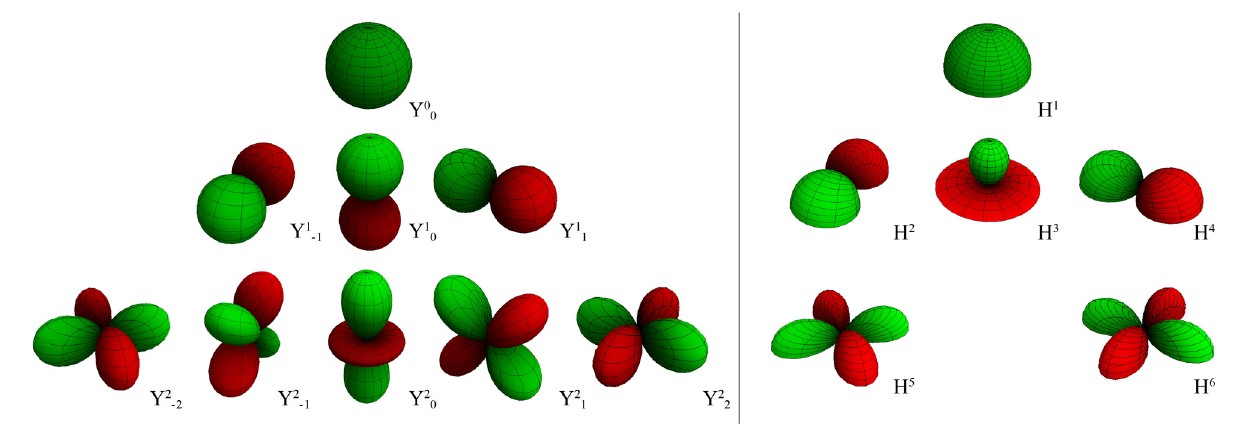
HSH light coefficients
H0 = 1 / sqrt(2π)
H1 = sqrt(6/π)(cos(φ) sqrt(cos(θ)-cos(θ)2))
H2 = sqrt(3/(2π))(2cos(θ)-1)
H3 = sqrt(6/π)(sqrt(cos(θ) - cos(θ)2)sin(φ))
H4 = sqrt(30/π)(cos(2φ)(-cos(θ) + cos(θ)2))
H5 = sqrt(30/π)(cos(φ)(2cos(θ)-1)sqrt(cos(θ) - cos(θ)2))
H6 = sqrt(5/(2π))(1 - 6cos(θ) + 6cos(θ)2)
H7 = sqrt(30/π)((2cos(θ)-1)sqrt(cos(θ) - cos(θ)2)sin(φ))
H8 = sqrt(30/π)((-cos(θ) + cos(θ)2)sin(2*φ))
HSH
R(l) = r0H0(l) + ... + r8H8(l)
G(l) = g0H0(l) + ... + g8H8(l)
B(l) = b0H0(l) + ... + b8H8(l)
Requires 27 coefficients
RTI Compression
- Coefficients scaled and quantized (8 bits)
- JPEG encoding
RAW: 80MB
HSH: 3.0MB
PTM: 1.9MB
LPTM: 1.4MB
RTI Rendering
Texture lookup, dequantization, light coefficients.
uniform sampler2D planes[6];
uniform float light[6], bias[6], scale[6];
varying vec2 v_texcoord;
void main(void) {
vec3 color = vec3(0);
for(int j = 0; j < 6; j++) {
vec4 c = texture2D(planes[j], v_texcoord);
color.x += light[j]*(c.x - bias[j*3+0])*scale[j*3+0];
color.y += light[j]*(c.y - bias[j*3+1])*scale[j*3+1];
color.z += light[j]*(c.z - bias[j*3+2])*scale[j*3+2];
}
gl_FragColor = vec4(color, 1.0);
};
Used mostly in Cultural Heritage
- Inscriptions
- Cuneiform tablets
- Manuscripts
- Coins
- Small manufacts
Cheap, captures well the appearance
Both an inspection and a presentation tool
CHI

- Training, consulting.
- RTIBuilder
- RTIViewer
http://culturalheritageimaging.org/Technologies/RTI/
Web RTI Viewer

- Tiled approach
- Supports .PTM and .HSH
- Open source
http://vcg.isti.cnr.it/rti/webviewer.php
dhlab-basel/rti.js
- IIIF compliant
- Supports .PTM
- three.js
- Open source
https://github.com/dhlab-basel/rti.js
Improving quality/size ratio
Radial Basis Function (RBF)

Multispectral RTI analysis of heterogeneous artworks, Giachetti et.al.
RBF
- Very good RTI fidelity
- Requires ALL the original images!
RBF (approximated)

We need to approximate the array [ρ1 ... ρN]
for each pixel.
Principal component analysis (PCA)

Distributive property!

Same computational cost
- Compute light coefficients once
(this time using a small vector base)
- Weighted sum for each pixel.
A custom base using PCA

and PCA neglected the color red.
Luminance-Chroma decoupling
Convert images to YCbCr

Luminance vs Croma fidelity

Custom sampled basis
What if the light direction is not constant in our sampling?
or we compute a custom base in some other way?
Bilinear interpolation
The function is resampled with over a grid (9x9)
and costant for all pixels.

Half sphere to square?
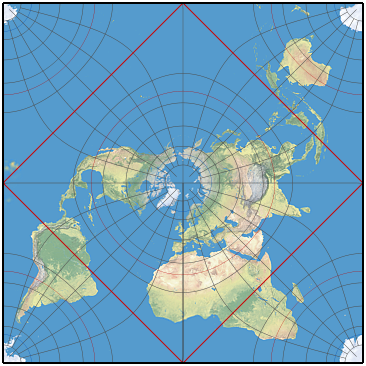
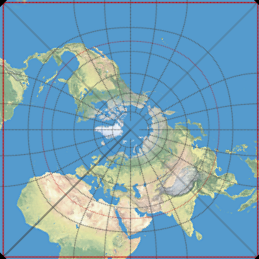
Flattened octahedron projection
Bilinear resampling (1)
We need to find 81 values such that when interpolated
the surface is as closed as possible to the original samples
- N original samples ρi
- M grid resamples ηj
Minimize |Aη - ρ|2 where A is the bilinear interpolation matrix
Bilinear resampling (2)
Tikhonov regularization, since we have a prior ( and N < M happens)
Rρ = η0 ( R is the RBF coefficient matrix)
Minimize |ρ − Aη|2 + τ|η − η0|2
Then build a basis using PCA

or any other algorithm...
Same rendering algorithm

Bonus: texture access with bilinear interpolation

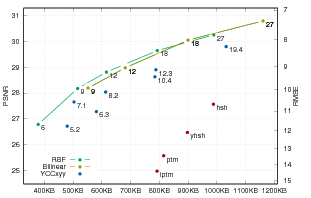
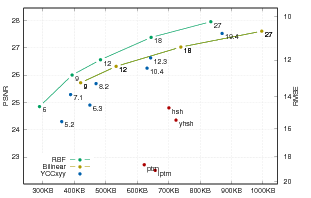
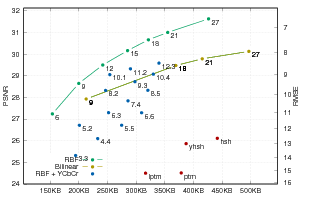
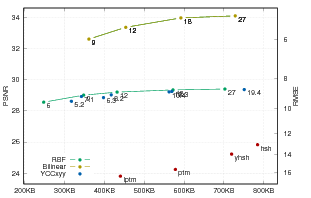
PTM mse [0,25]

HSH

RBF
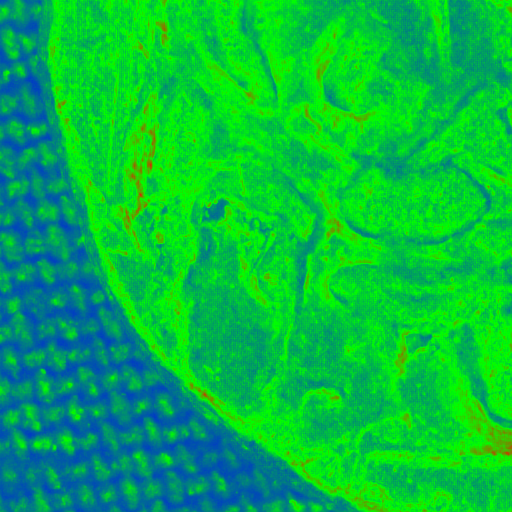
BILINEAR
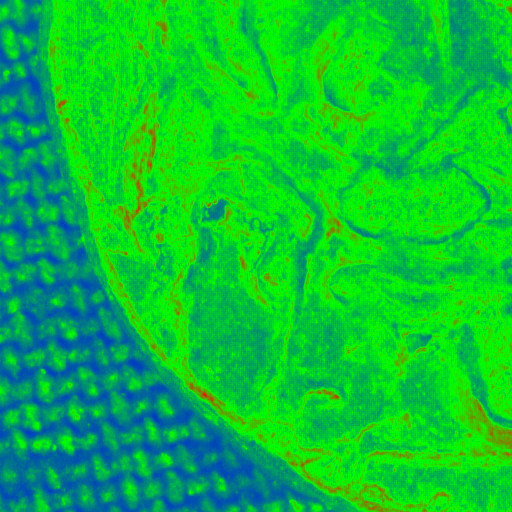
WebGL rendering changes
Custom base is delivered in JSON (~5-40Kb)
Light dependent coefficients computed in Javascript
Conclusions
- Better quality/size ratio
- Same computational cost (same opengl code!)
- Luma-chroma optimization
- Flexible: any sampled base.