Compression and Querying of Arbitrary Geodesic Distances
Lecture Notes in Computer Science - special issue of ICIAP 2015, Volume 9279, page 282--293 - August 2015
Download the publication :
![paper.pdf [5.5Mo]](/Publications/images/pdf.png)
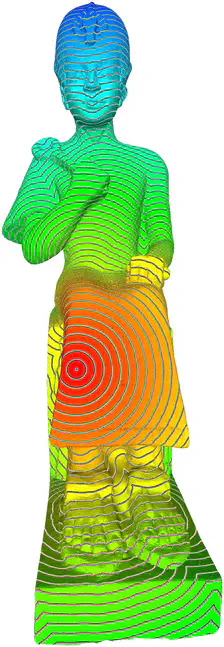
In this paper, we propose a novel method for accelerating the computation of geodesic distances over arbitrary manifold triangulated surfaces. The method is based on a preprocessing step where we build a data structure. This allows to store arbitrary complex distance metrics. We show that, by exploiting the precomputed data, the proposed method is significantly faster than the classical Dijkstra algorithm for the com- putation of point to point distances. Moreover, as we precompute exact geodesic distances, the proposed approach can be more accurate than state-of-the-art approximations.
Iciap presentation
Images and movies
![ramessesmsad_exactfront_crop.png [203Ko]](/Publications/2015/ABPMCS15/ramessesmsad_exactfront_crop.png){kind=small}
BibTex references
@Article\{ABPMCS15,
author = "Aiello, Rosario and Banterle, Francesco and Pietroni, Nico and Malomo, Luigi and Cignoni, Paolo and Scopigno, Roberto",
title = "Compression and Querying of Arbitrary Geodesic Distances",
journal = "Lecture Notes in Computer Science - special issue of ICIAP 2015",
volume = "9279",
pages = "282--293",
month = "August",
year = "2015",
note = "DOI: 10.1007/978-3-319-23231-7 26",
url = "http://vcg.isti.cnr.it/Publications/2015/ABPMCS15"
}