Geometry Processing
Our research focuses on concepts and practical algorithms for the creation and manipulation of digital shape representation.
Mesh Parametrization
Parametrization is commonly defined as a bijective mapping between a two-dimensional domain and a two-manifold surface embedded in R3. "Good" parameterizations are a prerequisite in modelling and rendering techniques, like remeshing, morphing, texture mapping and others.

Robust Field-aligned Global Parametrization present a robust method for computing locally bijective global parametrizations aligned with a given cross-field.

Global Parametrization of Range Image Sets allows to globally parameterize a surface represented by range images. In contrast to other parameterization techniques, we do not start with a manifold mesh. Construction of such global parameterization requires only a way to project surface data onto a set of planes, and can be applied directly to implicit surfaces, nonmanifold surfaces, very large meshes, and collections of range scans.

Simple Quad Domains technique preserves alignment to a cross field in input while obtaining a parametric domain made of few coarse axis-aligned rectangular patches,which form an abstract base complex without T-junctions.
Modeling
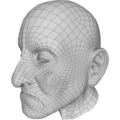
An interactive quadrangulation method based on a large collection of patterns that are learned from models manually designed by artists.
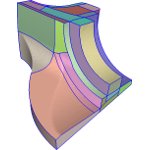
Feature-aligned T-meshes proposes an approach to constructing patch layouts consisting of small numbers of quadrilateral patches while maintaining good feature alignment. To achieve this, we use quadrilateral T-meshes, for which the intersection of two faces may not be the whole edge or vertex, but a part of an edge
Architectural geometry

A framework for the generation of polygonal grid-shell architectural structures, whose topology is designed in order to excel in static performances.