3D GEOMETRIC MODELING & PROCESSING 2024/2025

Paolo Cignoni

Syllabus

The course begins by laying the theoretical foundations for treating 3D surfaces and shapes in mathematics and computer science. The framework of simplicial complexes and the basics of differential geometry and topology are presented to students with a flavour oriented to computer graphics applications. Subsequently, the main data structures for the management of discrete representations of surfaces are described together with introduces an overview of data structures for the efficient management of spatial queries.

On this basis, the main geometry processing algorithms are introduced together with their practical applications. During the course, exercises will be conducted on the topics discussed by examining and presenting both low-level (C ++) implementations of data structures and algorithms and python libraries that allow rapid prototyping of applications that can solve complex geometric problems.

By the end of the course, the students will be able to use the most appropriate geometry processing algorithms and data structure to solve the problems that can arise when handling 3D geometric shape representations. The theoretical background and the good knowledge of the geometrical properties of surfaces will be useful for a better comprehension of the pitfalls and limitations that can be encountered when handling real world problems where surfaces and 3D representations are involved, like the one that can be encountered in computer aided design, interactive computer graphics and industrial design.

  • Discrete Representations for Surfaces
  • Data Structures for Simplicial Complexes and spatial Indexing
  • Basics of Differential Geometry and Topology for Computer Graphics
  • Mesh Processing Algorithms
  • Remeshing, Refinement & Simplification
  • Parametrization and Texturing
  • Fairing and Smoothing
  • Surface reconstruction and Sampling
  • 3D Geometry Representation and Processing for Learning

    Examination

    The exam consists of a practical part and a theoretical part.

    TimeTable

    Lunedì Martedì Mercoledì Giovedì Venerdì
    16:00 - 18:00
    Aula Fib C1     		16:00 - 18:00
    Aula Fib 1 Lab

    Lezioni e Lucidi

    Data Contenuto
    26 09 2024 Lunedì 16:15 18:00 Introduction to the course. PDF
    Representing Surfaces PDF
    28 09 2024 Mercoledì 16:15 18:00 Representing Surfaces (second part)
    30 09 2024 Lunedì 16:15 18:00 First Experiments with VCGLib
    PDF The code shown at lessons for calculating Euler's characteristic and walking on boundary loops is contained in this archive GP20240930.zip. The cmakelist expects that you have a folder vcglib containing a clone of the github repo of vcglib (branch devel). The meshes shown during the lesson are contained in mesh.zip.
    02 10 2024 Mercoledì 16:15 18:00 Meshing Surfaces PDF
    07 10 2024 Lunedì 16:15 18:00 Reimplementing Catmull Subdivision
    The code shown at lessons for computing Catmull Clark Subdivision is contained in this archive GP20241007.zip. The cmakelist expects that you have a folder vcglib containing a clone of the github repo of vcglib (branch devel). As exercise try to compute the correct position of the vertex of the original mesh using this simple weighing scheme where the red empty dot is the face barycenter. For a quad mesh it is equal to the weights shown at lesson. Eg. according to the illustration if you consider an edge \(v_0, v_1\) where the vertexes adjacent to the edge on the two faces are \(f_{00} f_{01} \) and \( f_{10} f_{11}\), you have that the edge vertex position is \(p = v_0+v_1+1/4 \cdot (v_0+v_1+f_{00}+f_{01}) +1/4 \cdot (v_0+v_1+f_{10}+f_{11})\) that is equal (after normalization) to the \( 6 v_0 + 6 v_1+f_{00}+f_{01}+f_{10}+f_{11} \)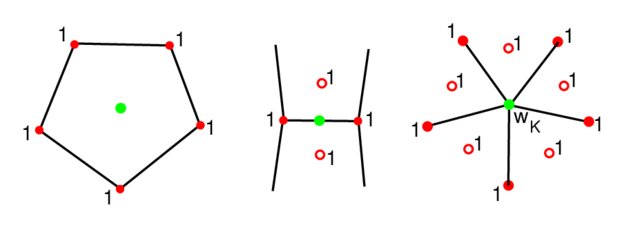
    09 10 2024 Mercoledì 16:15 18:00 Spatial Indexing PDF
    14 10 2024 Lunedì 16:15 18:00 Implementing a Catmull Subdivision filter for Meshlab
    The code shown at lessons (refeactoring the previous example in a static templated class and using it a MeshLab filter) is contained in these two commits done to the vcglib and to the Meshlab github repositories.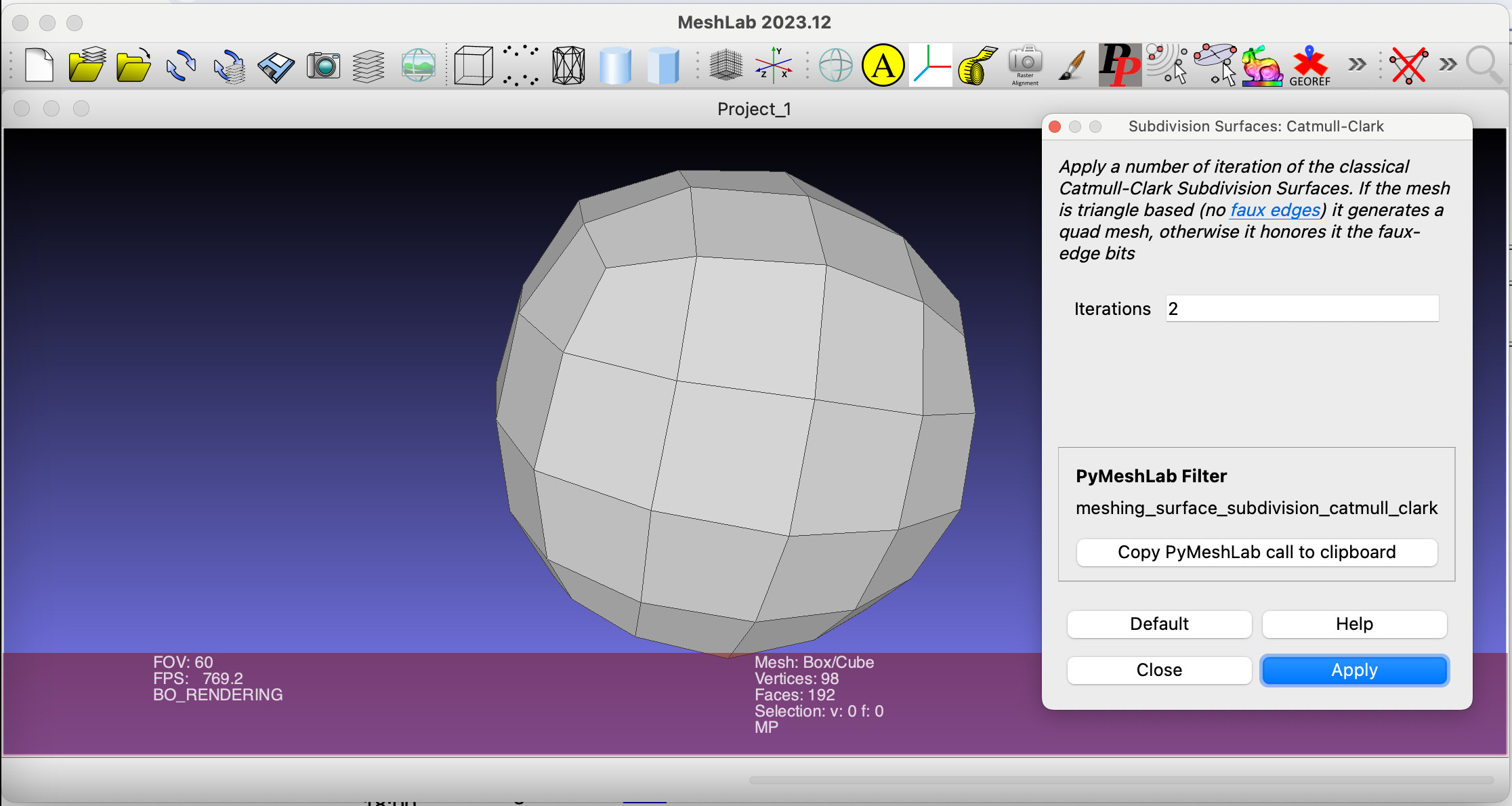
    16 10 2024 Mercoledì 16:15 18:00 Sampling PDF
    21 10 2024 Lunedì 16:15 18:00 Starting the Voronoi Weaving project.
    The main idea is to adapt the existing framework for computing Voronoi Diagfram over meshes in order to compute Weaving Voronoi diagrams. Weaving Voronoi diagrams are VDs that stays far from themselves when the surface self intersect. Discussion on possibile strategies of how implement it and collecting datasets for testing. The meshes created at lesson are here , and the code of the basic example for computing simple VD over a mesh is here .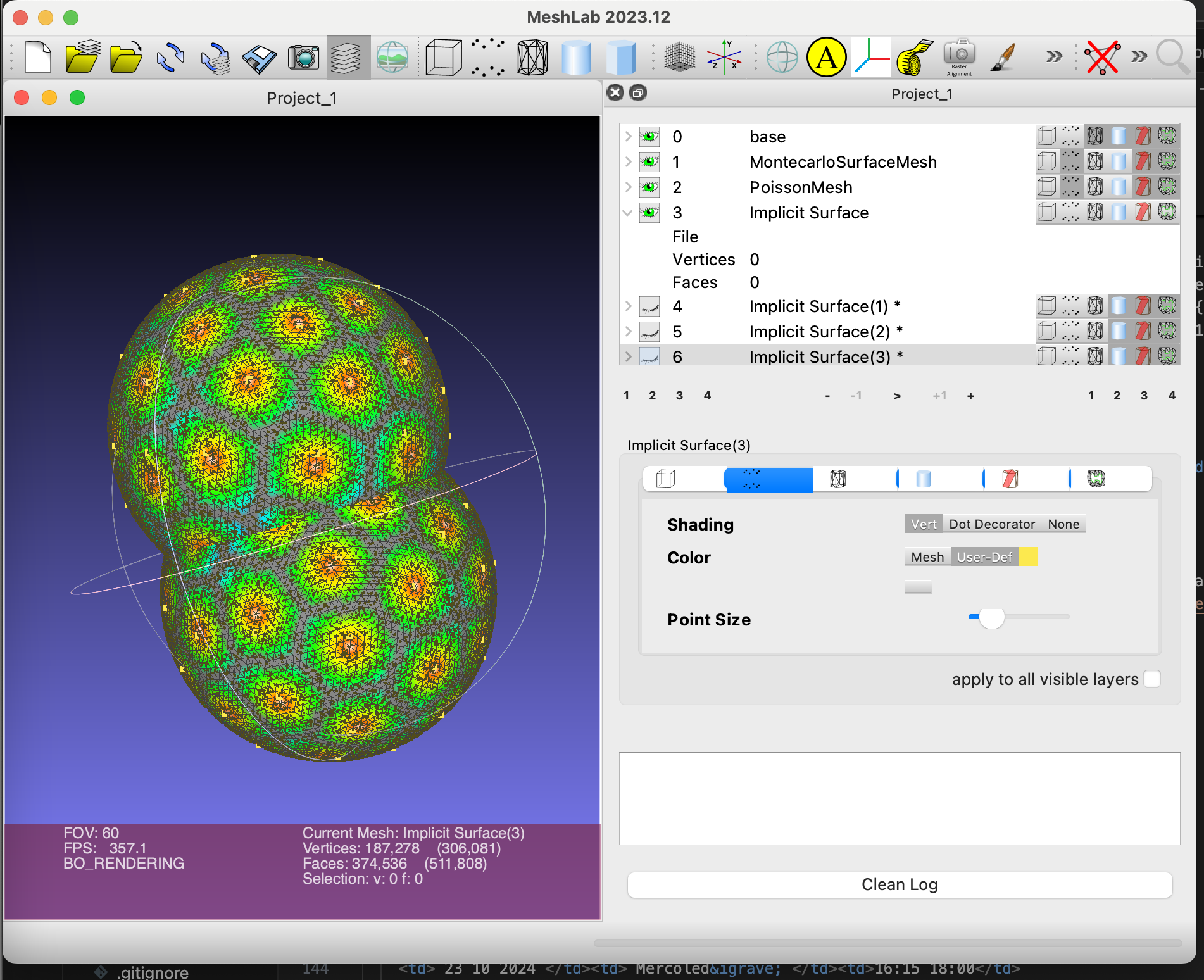
    23 10 2024 Mercoledì 16:15 18:00 Differential Geometry PDF
    28 10 2024 Lunedì 16:15 18:00 Voronoi Weaving project.
    Today the main point was to validate the intuition that vertexes of the surface having in the euclidean neighbourhood some vertex whose geodetic distance is quite different from the euclidean one, are the ones that are more likely to be in the weaving Voronoi diagram are good candidate of being close to a self intersection. The code shown at lesson is here . We did some very simple assumptions: we used graph distance instead of geodesic and we limited to a small neighbourhood (two or three hops).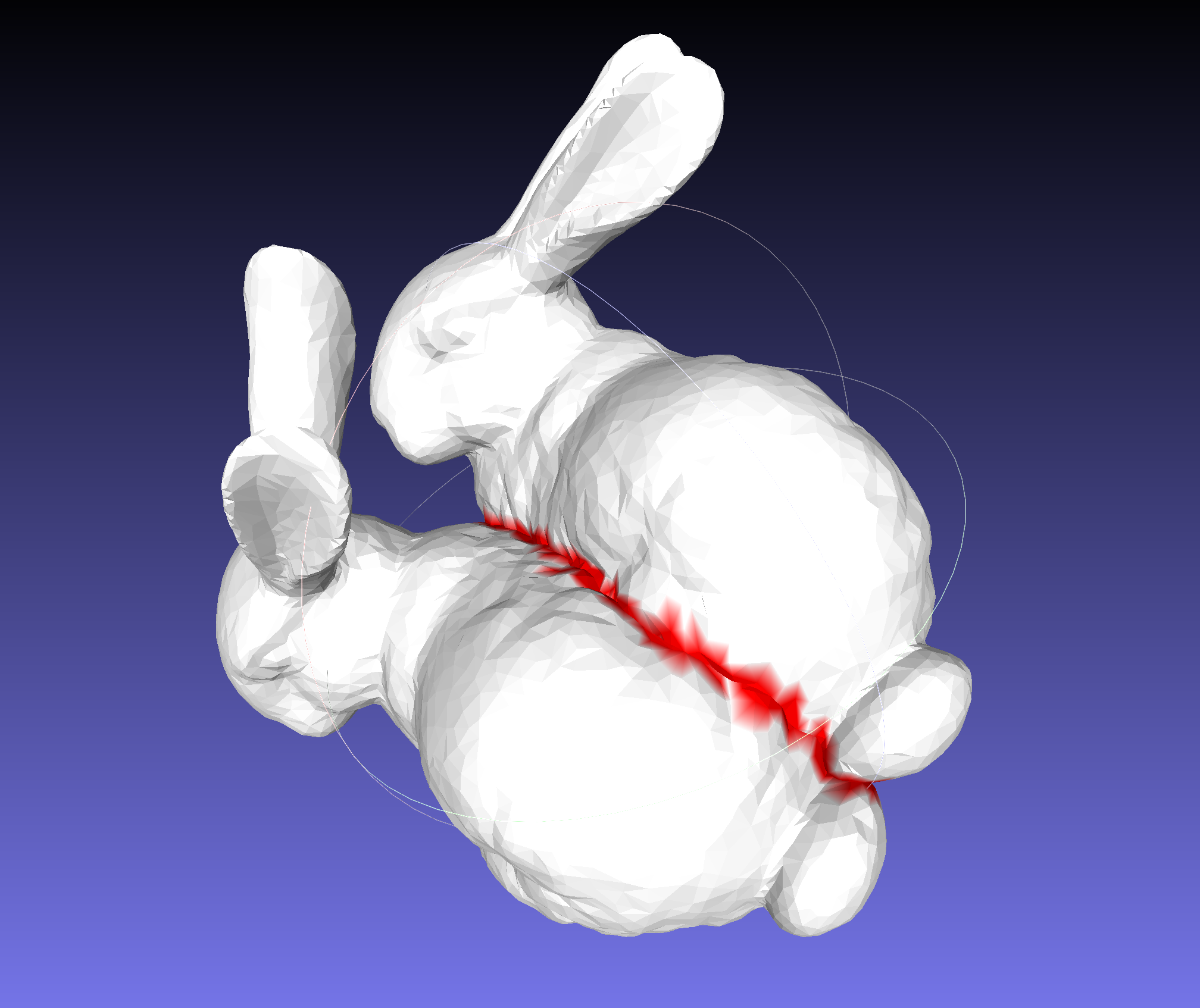
    30 10 2024 Mercoledì 16:15 18:00 Surface Reconstruction PDF & PDF